library(ggplot2)
library(ggthemes)
library(dplyr)

df <- data.frame(party = c("kesk", "sde", "ekre", "vaba", "ref", "irl"),
                 lrScale = c(-7.8, -7.8, -0.6, 2.2, 4.4, 3.3),
                 conlibScale = c(3.1, 5.6, -9.4, 1.9, 0.6, -3.8),
                 seats = c(27, 15, 7, 8, 30, 14))

df %>% ggplot() +
  aes(lrScale, conlibScale) +
  geom_point() +
  geom_text(aes(label=paste0(party, " ", seats)), hjust=-.3, vjust=.3) +
  coord_cartesian(xlim=c(-10,10), ylim=c(-10, 10)) +
  xlab("vasak-parem") + ylab("konservatiivne-liberaalne") +
  theme_minimal() +
  theme(aspect.ratio = 1,
        legend.position = "right",
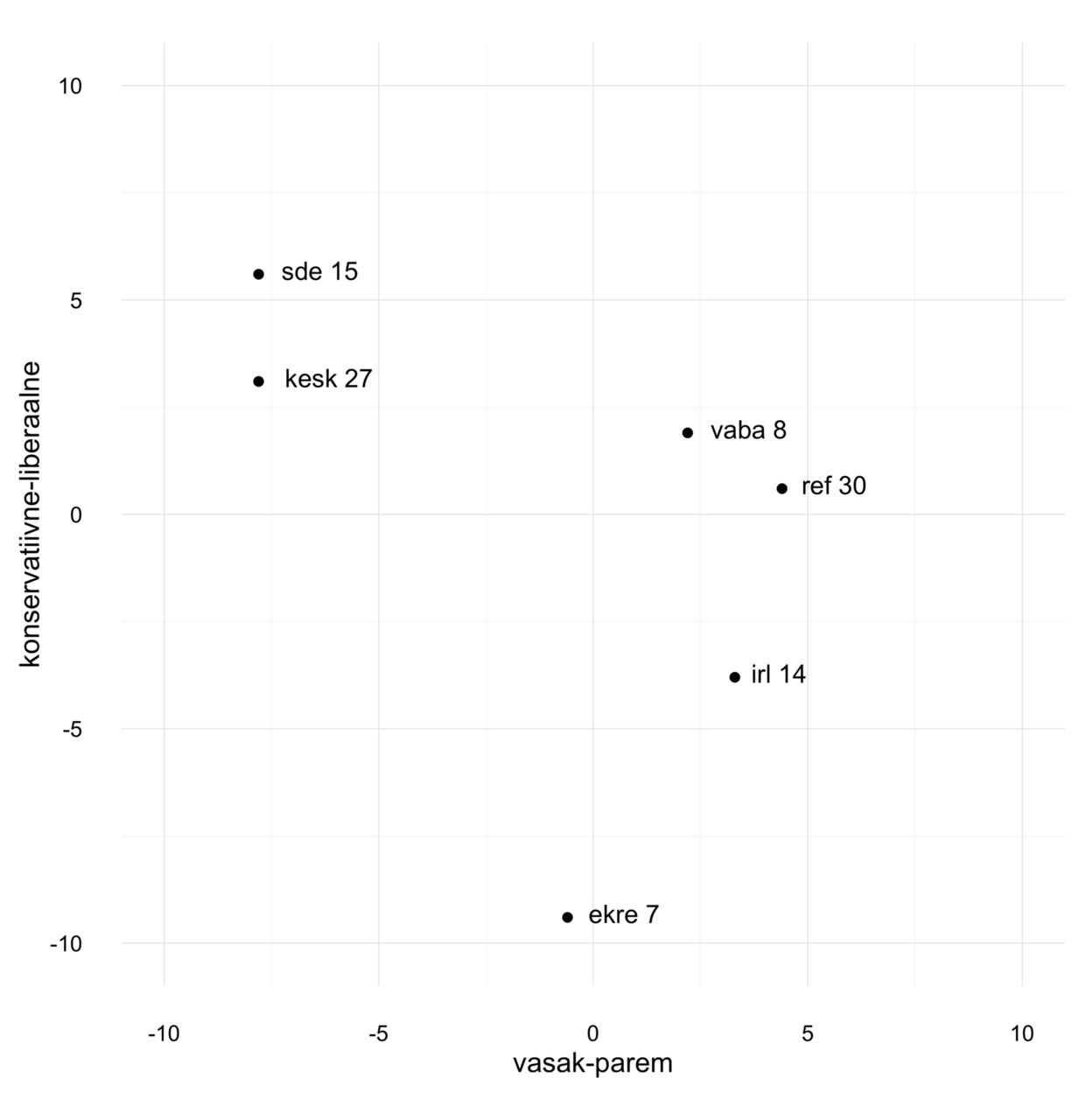
        plot.background = NULL)

Ratsionaalsed valikud kõnelustel

Seega tuleks mõlema poliitilise maastiku dimensiooni puhul vaadata, millised erakonnad võiksid mängida majandus- ja väärtusskaalal võtmerolli, ehk millised erakonnad moodustavad dimensioonide mediaanid. Mediaanide leidmiseks loome uued erakondade mandaatidega kaalutud vektorid. Tinglikult tähistab see, kui suur häälejõud on antud maastikupunktil. Seejärel saab leida telgede mediaanid ning erakondade kaugused mediaanist.

# x-telje kaalutud vektor
wx = c(rep(df[1,]$lrScale, df[1,]$seats),
       rep(df[2,]$lrScale, df[2,]$seats),
       rep(df[3,]$lrScale, df[3,]$seats),
       rep(df[4,]$lrScale, df[4,]$seats),
       rep(df[5,]$lrScale, df[5,]$seats),
       rep(df[6,]$lrScale, df[6,]$seats))

# y-telje kaalutud vektor
wy = c(rep(df[1,]$conlibScale, df[1,]$seats),
       rep(df[2,]$conlibScale, df[2,]$seats),
       rep(df[3,]$conlibScale, df[3,]$seats),
       rep(df[4,]$conlibScale, df[4,]$seats),
       rep(df[5,]$conlibScale, df[5,]$seats),
       rep(df[6,]$conlibScale, df[6,]$seats))

df <- df %>% mutate(medianX = median(wx),
                    medianY = median(wy),
                    r = sqrt((lrScale - medianX)^2 + (conlibScale - medianY)^2)) # Kaugus mediaanpunktist

Keskendudes esialgu ainult poliitilise maastiku majandusskaalale, on mediaanis asuvaks erakonnaks Vabaerakond. Vabaerakonna toetus oleks vajalik temast nii vasakul kui paremal asetsevatele erakondadele, kui viimased soovivad teha koostööd just lähimate partneritega ja saavutada parlamendienamuse. Vastasel korral peaksid valitsuse moodustama teineteisest juba kaugemal asetsevad erakonnad (nagu juhtus REF+SDE+IRL valitsusega), mis ei pruugi olla kõige stabiilsem kooslus. Mediaanis asetseval erakonnal on sellest tulenevalt hea positsioon koalitsioonikõnelustel osalemiseks, sõltumata otseselt valimistel saadud mandaatide arvust.

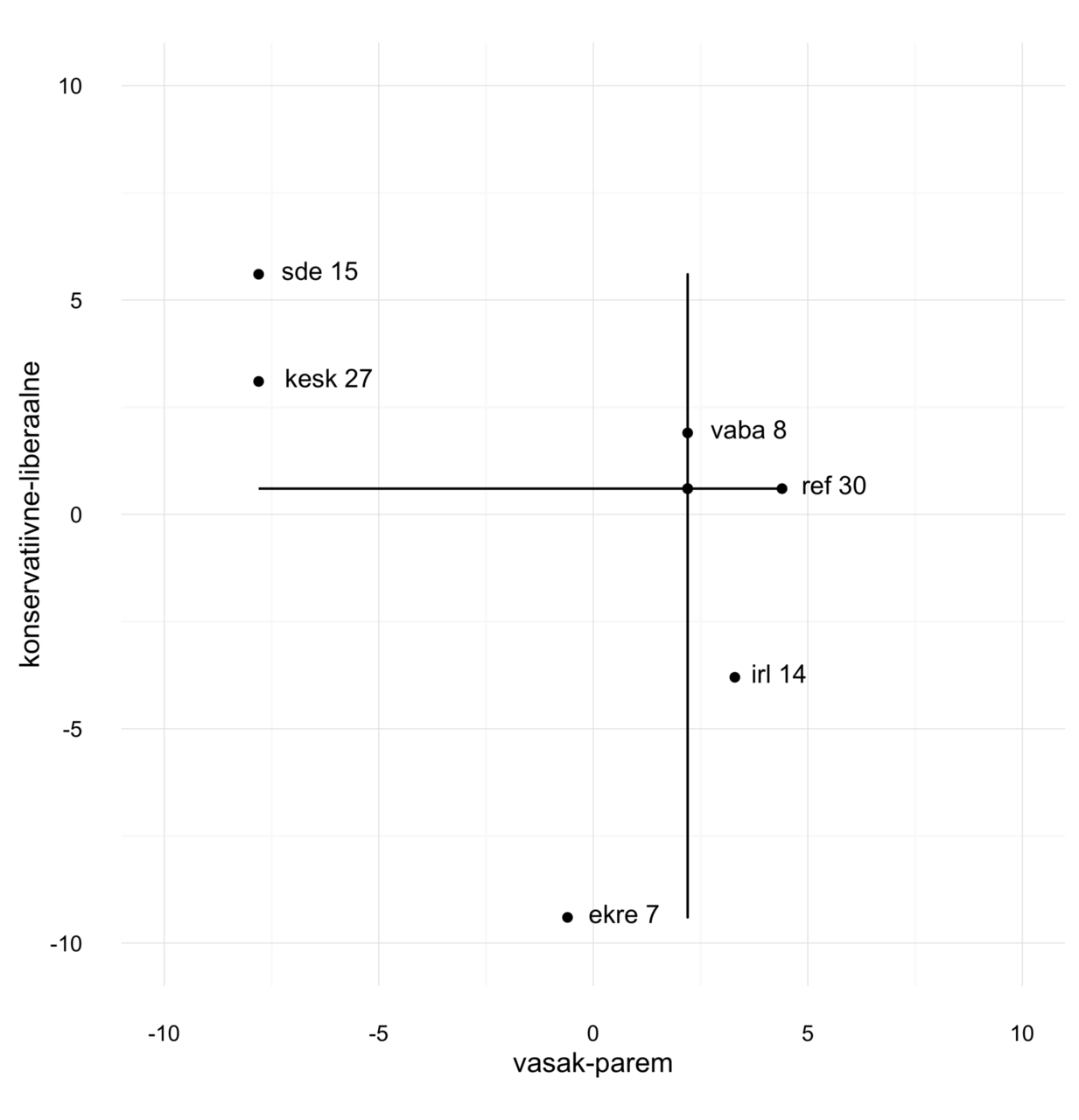
Lisades juurde poliitilise maastiku väärtusskaala, selgub, et teine mediaanis asetsev erakond on Reformierakond.

df %>% ggplot() +
  aes(lrScale, conlibScale) +
  geom_point() +
  geom_text(aes(label=paste0(party, " ", seats)), hjust=-.3, vjust=.3) +
  geom_line(aes(lrScale, median(wy))) +
  geom_line(aes(median(wx), conlibScale)) +
  geom_point(aes(median(wx), median(wy))) +
  coord_cartesian(xlim=c(-10,10), ylim=c(-10, 10)) +
  xlab("vasak-parem") + ylab("konservatiivne-liberaalne") +
  theme_minimal() +
  theme(aspect.ratio = 1,
        legend.position = "right",
        plot.background = NULL)

Mediaanide ristumispunkt (edaspidi mediaanpunkt) tähistab kõige tugevamat strateegilist positsiooni, mida küll ükski erakond ei täida, aga mis oleks läbirääkimiste seisukohast parim võimalik asukoht. Seega peavad kõik erakonnad (k.a Vabaerakond ja Reformierakond) olema antud kahe dimensiooni raames mingil määral järeleandlikud.

Järeleandmisi tasub teha kuni määrani, mis ei ületa parimat läbirääkimiste positsiooni ehk mediaanpunkti. Järeleandmiste tulemusel mediaanpunktile lähenedes kaugenevad erakonnad küll oma programmilistest seisukohtadest (negatiivne mõju), aga saavutavad läbi selle tugevama läbirääkimiste positsiooni (positiivne mõju). Minnes mediaanpunktist edasi, hakkab kaugenemise negatiivne mõju kaaluma üle läbirääkimisjõu positiivset mõju (seda võib mõista läbi Nashi tasakaalu). Mediaanpunkt on seega optimaalne piir, mille raames võivad erakonnad kompromisse teha.

Lihtsustatult võime antud mõtteharjutuse raames eeldada, et teades oma kaugust mediaanpunktist, võivad erakonnad liikuda poliitilisel maastikul erinevates suundades leitud distantsi piires. Teisisõnu: erakondadel ei ole tugevat eelistust, kas ta kaldub mõnevõrra vasakule-paremale või konservatiivsemaks-liberaalsemaks, kui see tagab kokkuvõttes koha valitsuses.

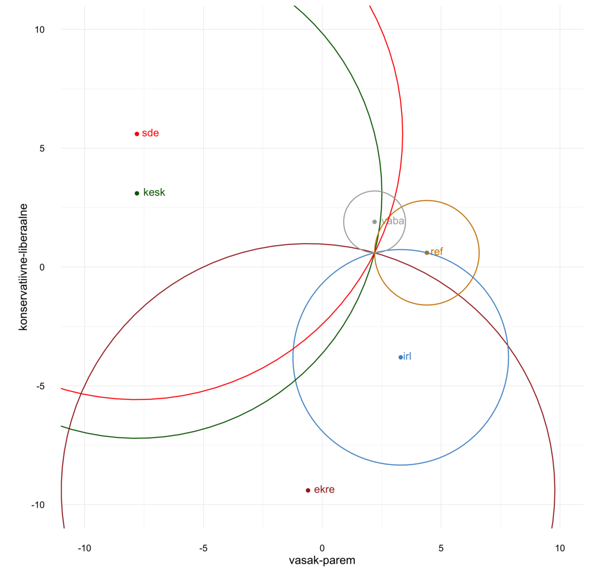
Selle mõtte paremaks visualiseerimiseks võime joonistada erakondadele mediaanpunktiga lõikuvad ringid. Ringide sisse jääv ala tähistab mõttelist ruumi poliitilisel maastikul, mille raames on erakondadel otstarbekas läbirääkimistesse asuda. Ringide loomiseks kasutame funktsiooni, mis arvutab ringjoone punktväärtused, ning seejärel ühendame arvutatud punktid joonega.

# Funktsiooni sisenditeks on ringi keskpunkti koordinaadid, raadius ja erakonna tunnus
circleCoord <- function(center = c(0,0), r, party){
  tt <- seq(0,2*pi,length.out = 100)
  xx <- center[1] + r * cos(tt)
  yy <- center[2] + r * sin(tt)
  return(data.frame(x = xx, y = yy, party = party))
}

# Funktsioon jooksutatakse iga erakonna kohta ning salvestatakse listi
circlesData <- lapply(c(1:nrow(df)), function(x){
  circleCoord(c(df$lrScale[x], df$conlibScale[x]), df$r[x], df$party[x])
})

# List ühendatakse ühtseks data frame'iks
circlesData <- do.call("rbind", circlesData)

Graafime tulemused!

circlesData %>% ggplot() +
  aes(x,y, color=party) +
  geom_point(data=df, aes(lrScale, conlibScale)) +
  geom_text(data=df, aes(lrScale, conlibScale, label=party), hjust=-.3, vjust=.3) +
  coord_cartesian(xlim=c(-10,10), ylim=c(-10, 10)) +
  geom_path() +
  scale_color_manual(values = c("brown", "steelblue3", "darkgreen", "orange3", "red", "darkgrey")) +
  xlab("vasak-parem") + ylab("konservatiivne-liberaalne") +
  theme_minimal() +
  theme(aspect.ratio = 1,
        legend.position = "",
        plot.background = NULL)

• esiteks on kõige lihtsam jõuda kokkulepeteni, kui erakondade huvisfäärid (joonistatud ringid) on omavahel kattuvad. Kattuvad alad tähistavad poliitilisel maastikul piirkondi, kus kõik osapooled tunnevad end võrdlemisi mugavalt;
• teiseks on vaja, et omavahel kattuvad erakonnad moodustaksid parlamendis enamuse, mis võimaldab neil oma kavandatavat poliitikat teostada;
• kolmandaks ei tohiks koalitsiooni kaasata üleliigseid erakondi, kuna see toob üldjuhul kaasa liigsete kompromisside tegemise ja muudab loodava koalitsiooni ebastabiilsemaks.

Loodud ringide kattuvuste leidmiseks, mis rahuldaksid ühtlasi enamusvalitsuse tingimuse, on erinevaid meetodeid. Üks oleks luua n-dimensionaalne maatriks, milles oleks arvutatud kõik võimalikud erakondadevahelised kombinatsioonid. Teine võimalus on katta poliitiline maastik andmepunktidega, ning hinnata punktide kattuvust varasemalt arvutatud ringidega. Teades seejuures, milliste ringide sisse punkt asetub, on võimalik arvutada seotud erakondade mandaatide arv: teisisõnu, kas antud punktis on kaetud parlamendi enamus.

Kuigi teine nimetatud variantidest annab vaid ligikaudse hinnangu erakondade omavahelise kattuvuse hindamiseks, on tulemused piisavalt suure hulga andmepunktide korral siiski võrdlemisi täpsed. Ühtlasi, kuna teine variant on oluliselt lihtsamini teostatav - kasutame seda!

# Tühi data frame loodavate andmepunktide talletamiseks. Hiljem kustutame esialgse tühja rea
scattered <- data.frame(x = NA, y = NA, ref = NA, kesk = NA, sde = NA, irl = NA, vaba = NA, ekre = NA, sum = NA, majority = NA, party = NA)

# Funktsioon punktide ja erakonna ringide kattuvuse tuvastamiseks
partyDistance <- function(x, y, party){
  tmp <- df[df$party == party,]$r >= sqrt((x - df[df$party == party,]$lrScale)^2 + (y - df[df$party == party,]$conlibScale)^2)
  return(tmp)
}

# Andmepunktide tihedus. Mida väiksemat sammu kasutada, seda täpsemad tulemused, ent seda kauem kood jookseb
step <- .05
# Asetame andmepunktid maastikule. Optimeerimise eesmärgil võib telgede piirmäärasid nihutada 
coordinatesX <- seq(-2,7,step)
coordinatesY <- seq(-4,2.5,step)
for(i in 1:length(coordinatesY)){
  for(j in 1:length(coordinatesX)){
    coord <- data.frame(x = coordinatesX[j],
                        y = coordinatesY[i])
    
    # Arvutame, kas erakonnade ringid kattuvad andmepunktiga, mis on mandaatide summa, kas sellest piisab koalitsiooniks ning millised erakonnad sellesse panustavad
    coord <- coord %>% mutate(ref = ifelse(partyDistance(x, y, "ref"), df[df$party == "ref",]$seats, 0),
                              kesk = ifelse(partyDistance(x, y, "kesk"), df[df$party == "kesk",]$seats, 0),
                              sde = ifelse(partyDistance(x, y, "sde"), df[df$party == "sde",]$seats, 0),
                              irl = ifelse(partyDistance(x, y, "irl"), df[df$party == "irl",]$seats, 0),
                              vaba = ifelse(partyDistance(x, y, "vaba"), df[df$party == "vaba",]$seats, 0),
                              ekre = ifelse(partyDistance(x, y, "ekre"), df[df$party == "ekre",]$seats, 0),
                              sum = ref + kesk + sde + irl + vaba + ekre,
                              majority = ifelse(sum >= 51, TRUE, FALSE),
                              party = paste0(ifelse(ref>0,"ref ",""),
                                             ifelse(kesk>0,"kesk ",""),
                                             ifelse(sde>0,"sde ",""),
                                             ifelse(irl>0,"irl ",""),
                                             ifelse(vaba>0,"vaba ",""),
                                             ifelse(ekre>0,"ekre ",""),
                                             sum))
    
    # Ühendame ühtseks andmestikuks
    scattered <- rbind(scattered, coord)
  }
}
# Kustutame esialgse tühja rea
scattered <- scattered[-1,]

Vaatame võimalikke koalitsioone, mis annaksid parlamendis enamuse.

maxValue <- (20/step) * (20/step)
scatterTable <- scattered %>%
  group_by(coalition = party, majority, sum) %>%
  summarise(n = n()) %>%
  mutate(percent = n/maxValue*100) %>%
  filter(majority == TRUE) %>%
  select(coalition, percent) %>%
  arrange(desc(percent))

scatterTable

## Source: local data frame [7 x 3]
## Groups: coalition, majority [7]
## 
##   majority                 coalition  percent
##      <lgl>                     <chr>    <dbl>
## 1     TRUE      kesk sde irl ekre 63 1.050000
## 2     TRUE           ref irl ekre 51 0.978125
## 3     TRUE           ref sde vaba 53 0.046875
## 4     TRUE      ref kesk sde vaba 80 0.006875
## 5     TRUE     kesk sde vaba ekre 57 0.004375
## 6     TRUE           ref irl vaba 52 0.001875
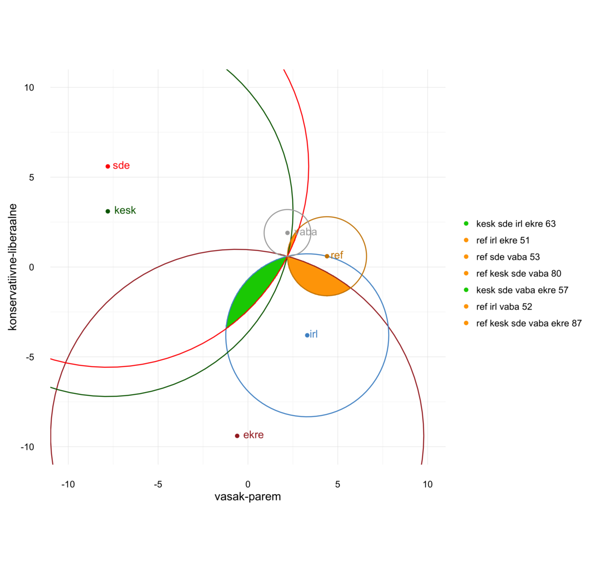
## 7     TRUE ref kesk sde vaba ekre 87 0.000625

Ülal olev tabel on järjestatud kattuva ala suuruse alusel (suuremast väiksemaks). Kõige suurem kattuvus on seejuures grupis “kesk sde irl ekre 63” (1.05% kogu maastikust), siis grupis “ref irl ekre 51” (0.98% kogu maastikust). Järgnevates gruppides on kattuvad alad ahtamad. Antud tulemuste puhul ei saa ennustada, milline koalitsioon moodustatakse, küll toob see välja võimalikud grupid, kus on antud kahe dimensiooni lõikes sobivamad eeldused koostööks.

Vaatame tulemusi graafiliselt.

circlesData %>% ggplot() +
  aes(x,y, color = party) +
  geom_point(data=scattered[scattered$majority == TRUE,], aes(x, y), size = .05) +
  geom_path() +
  geom_point(data=df, aes(lrScale, conlibScale)) +
  geom_text(data=df, aes(lrScale, conlibScale, label=party), hjust=-.3, vjust=.3, show.legend = FALSE) +
  coord_cartesian(xlim=c(-10,10), ylim=c(-10, 10)) +
  scale_color_manual(values = c("brown", "steelblue3", "darkgreen", "green3", "green3", "orange3", "orange", "orange", "orange", "orange", "orange", "red", "darkgrey"),
                     breaks = c("kesk sde irl ekre 63",
                                "ref irl ekre 51",
                                "ref sde vaba 53",
                                "ref kesk sde vaba 80",
                                "kesk sde vaba ekre 57",
                                "ref irl vaba 52",
                                "ref kesk sde vaba ekre 87")) +
  xlab("vasak-parem") + ylab("konservatiivne-liberaalne") +
  theme_minimal() +
  guides(colour = guide_legend(override.aes = list(linetype = 0, size = 1.5))) +
  theme(aspect.ratio = 1,
        legend.position = "right",
        plot.background = NULL)

Keskerakonna, SDE ja IRLi koalitsioonil paistab joonist vaadates olevat arutelu ruumi küll. Kattuv ala asetub seejuures telgede keskpunkti lähedal, mis on ootuspärane tulemus, arvestades, et Keskerakond ja SDE on liberaalsed vasakpoolsed erakonnad ning IRL konservatiivne parempoolne erakond. Kuhu tegelik koalitsioonilepe paigutub, saame loodetavasti näha juba lähiajal.

Joonist ja varasemat tabelit analüüsides selgub lisaks, et koalitsioon, kus oleks üheaegselt nii ref, sde ja irl, ei pruugi teoreetiliselt ühtegi osapoolt rahuldada (kombinatsioon puudub). Seda võib pidada taustal meeles, meenutades keerulisi koalitsioonikõnelusi 2015. aastal ning praegust Rõivase valitsuse lagunemist.

Viimaks võib märkida, et toodud võimalikud koalitsioonid on tuletatud vaid erakondade positsioonist poliitilisel maastikul, mis ei kajasta kõiki ühiskonnas olulisi küsimusi. Teiseks on eeldatud, et erakonnad ei soovi teha üleliigseid järeleandmisi, mis ei tähenda, et see ei võiks empiiriliselt aset leida. Kolmandaks on näha, et algoritm ei võta arvesse minimaalsete koalitsioonide tingimust, ehk teatud gruppides võib olla üleliigseid erakondi. Näiteks on võimalik eemaldada grupist “kesk sde irl ekre 63” ekre ning säilitada seejuures Riigikogu enamus 56 häälega. Gruppide “ref kesk sde vaba 80” ja "ref kesk sde vaba ekre 87" puhul on võimalik juba rohkem erinevaid kombinatsioone moodustada.